円の面積は 半径×半径×円周率=面積 で求めることができます。 半径をr、円周率をπ、面積をSとすると S=πr 2 となります。円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデアが出現する。 上野(09)は「測る」というテーマに着目して, 多角形や円の面積,多面体や回転体の体積を求めるた めに必要な極限概念,カヴァリエリの原理,積分概念 底面の円に描いた黄色の直角三角形で,斜辺の長さは半径 に等しいから, 次に高さ は, のとき で傾きが の直線上にあるから, ここで は奇関数の積分だから0 は上半円の面積だから円錐の表面積 π r(r a)(r = 底面の半径、a = 母線の長さ) 球 の表面積 4 π r

中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
円 表面積 体積 公式
円 表面積 体積 公式- 円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p 円 表面積 公式円錐の表面積を求める公式は、S = πr(rR) で表されます ♦ このページでは、「公式を使う場合」と「使わない場合」に分け、円錐の表面積の求め方を例題と共に説明しています。 半径 6 の円の面積は $ \pi \times 6^2 = 36 \pi $、円周の長さは $ 2\pi R




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
元のものが直接には分からなくても,その微分が分かれば,積分によって面積 S (x) が求まります. 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V (x) で表し 中学数学球の表面積の求め方の公式を1発で覚える方法 球の表面積の求め方の公式はおぼえにくい?? こんにちは!この記事をかいているKenだよ。豚肉を今日もいためたね。 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積 円柱の体積、表面積の求め方はこれでバッチリ!←今回の記事 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!
円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 円の面積は、 「半径 × 半径 × 314」 (半径 × 半径 × 円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 例題②半径 5 cmの円の面積を求めて下さい 円を扇形に切って並べ直してみると 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるの円の面積 「半径×半径×円周率」で求められる円の面積。 いろいろな大きさの円の面積を計算してみよう。 動画で学ぼう! (NHK for School) 円の面積の求め方を、四角に直すことで原理から考える
円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付き半径 6 の円の面積は π ×62 = 36π π × 6 2 = 36 π 、円周の長さは 2πR = 2π ×6 = 12π 2 π R = 2 π × 6 = 12 π です。 よって弧の面積は、半径 6 の円の面積 36π 36 π に、「円周の長さ 12π 12 π に対する弧の長さ 4π 4 π の 割合 」をかけて求積公式(平面) a=面積 正方形 長方形 平行四辺形 その和をもって不平行四辺形の面積を算出してもよい。 a=面積 正六角形 正八角形 正多角形 円 a=面積 円分 欠 円 環 形 扇 形




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 SV = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin球の表面積の考え方の例 4πr² 4 3 円がぴったり 入る円柱 円がぴったり 入る円柱 球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める 具体物での実験をもとに公式を




球の表面積と体積の公式 数学fun




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 Ken 計算公式円錐の表面積の求め方がわかる3つのステップ 円錐の表面積の求め方の公式って?? こんにちは、この記事をかいているKenだよ。



1




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト
円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス
体積・表面積の公式や求め方、単位あり計算問題 21年2月19日 この記事では、「円柱」の公式(体積・表面積)や実際の求め方をできるだけわかりやすく解説していきます。 また、リットルなどの単位を含む計算問題なども紹介していきますので、この 円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう! 簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを 角錐 円錐の体積と表面積の公式 数学fun 球の体積と表面積 公式と計算問題と証明 Irohabook 円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 円錐の表面積 あんず学習塾のメモ




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




角錐 円錐の体積と表面積の公式 数学fun
球の表面積・・・4πr² r³を微分すると3r²になります。 つまり、球の体積を微分すると円の表面積の公式になります。 そもそも微分とは、『少しの増加の間の変化量』を表現しています。 円の面積のちょこっとの増加分は円の周りの長さに相当します。球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる指導法 高校生・数学3C 記事詳細 数学講師必見中学数学でも必須! 球の体積、表面積の覚え方と導出まとめ! 高校数学 31,677 views 14年06月21日公開 キーワード




球の表面積と体積の公式 数学fun




円錐の表面積 Youtube
円の直径D、半径r、円の面積Aを示しました。 下図の円について、直径から面積に変換してみましょう。 円の直径D=8cmです。よって円の面積Aは、 です(π=314で計算)。 円の直径から面積に変換する公式は、数学だけでなく物理や工学でも使います。必ず 円柱の表面積-2つの円の面積=側面積(展開図の長方形の部分)であることから 側面積=-4×4×314×2=(㎠)となります。 側面積のたての長さは cm、横の長さは半径4cmの円の円周の長さ(8×314)であることから ×8×314= よって、 = 高校数学 kanrinin 微分でつなげる円や球の公式 今回の内容の動画版です→球の体積公式の微分が表面積になっている理由 円の面積、円周の長さおよび球の体積、表面積は次のように計算できます。



1




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ 楕円の面積 の公式は、次ようになります。 楕円の面積 S=π・a・b 楕円は半径aの円を縦軸方向に b/a倍縮小(拡大)した図形 と考えることができます。 ですから、円の面積公式(π・r・r)の応用と考えると覚えやすいです。球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) \(\displaystyle \frac {6}{D \rho}\) 半分以上隠れている円の直径の推定 接触角の概算 円と球の空間




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




中1 数学 6 5 球の体積 表面積 Youtube
回転体の表面積も求めよう! では次,曲線をx 軸やy 軸のまわりに回転してできる回転体の曲面の表 面積を求める公式についても解説しておこう。 (Ⅰ) について,微小区間x, +Δ における 微小な曲面の表面積 ΔS は,図12 より 他の面積公式との関係 この面積公式をもとに他の面積公式を導出することができます。 例えば,この公式と正弦定理を用いることで対称な式: S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c を得ることができます( R R R は三角形 A B C ABC A BC の外接円の半径)。




角柱 円柱の表面積と体積の公式 数学fun



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
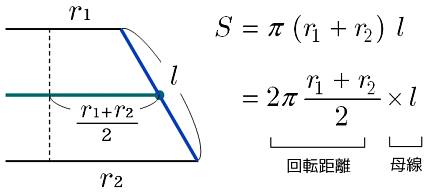



初等幾何 円錐台の側面積を求める 大人が学び直す数学
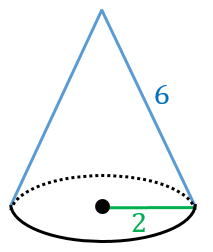



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




現役塾講師直伝 円錐の表面積を求める 裏技 Kouの学び部屋




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
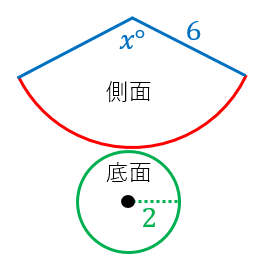



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




公式を図解 すい体の体積 円すいの表面積の求め方
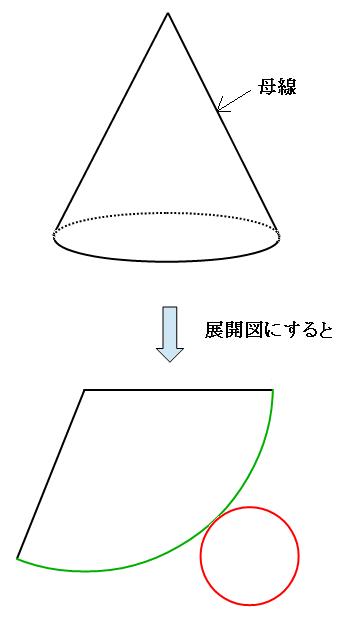



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




スタディピア 立体の表面積




投影図から円錐の表面積を求める方法がわかりません 答えと解説を詳しく教えてください Clear




円錐の表面積 Youtube




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




円錐の体積ってなんであの公式なの Webty Staff Blog




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋




表面積の求め方 計算公式一覧
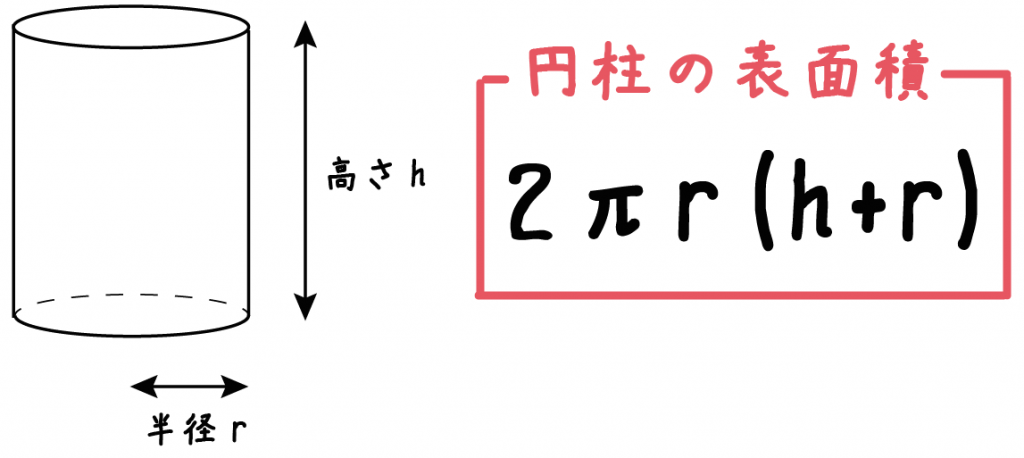



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor




球の表面積と体積の公式 数学fun




表面積の求め方 計算公式一覧



3




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円錐とは 体積 表面積の公式や求め方 受験辞典




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




球の体積と表面積 公式と計算問題と証明 Irohabook




球の体積と表面積 Youtube




球の表面積の公式について みたにっき はてな




半球の体積と表面積を計算する 具体例で学ぶ数学




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ
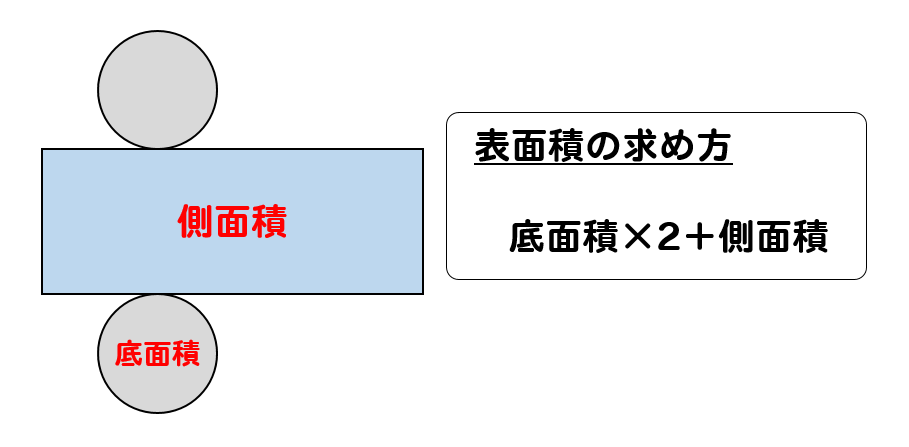



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円柱の表面積の求め方 公式と計算例




円錐の表面積の求め方 公式と計算例



球の表面積 アルキメデスの方法 4の2 セルフ塾のブログ
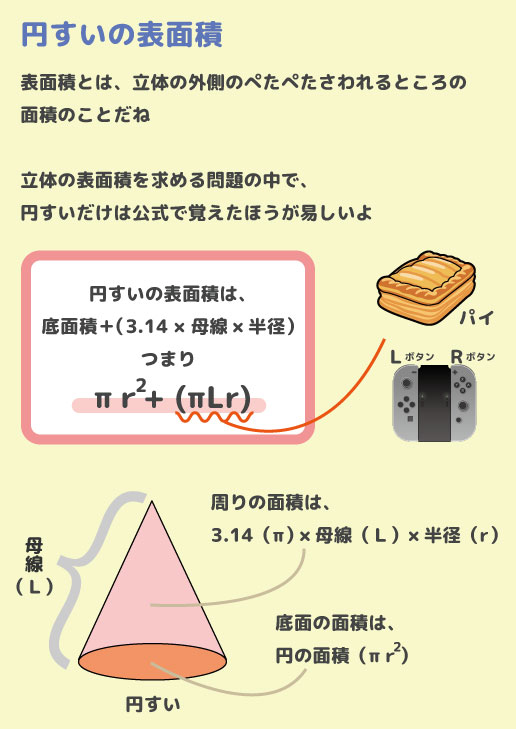



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強




体積 表面積まとめ記事 いろいろな図形の求め方を一気に学べる 高校生向け受験応援メディア 受験のミカタ




中1 数学 中1 立体の表面積 Youtube




円すいの展開図 表面積の求め方 公式があるの知っていますか
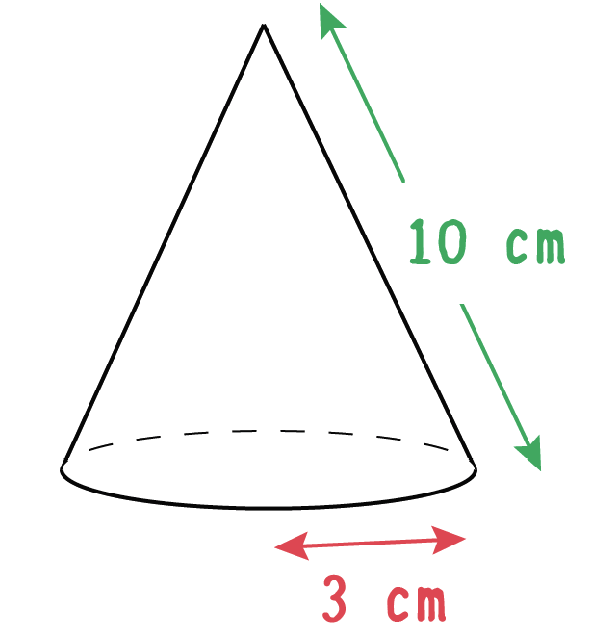



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




球表面積公式證明妙不可言的數學證明 Qavhp




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




初等幾何 球の表面積を求める 大人が学び直す数学




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
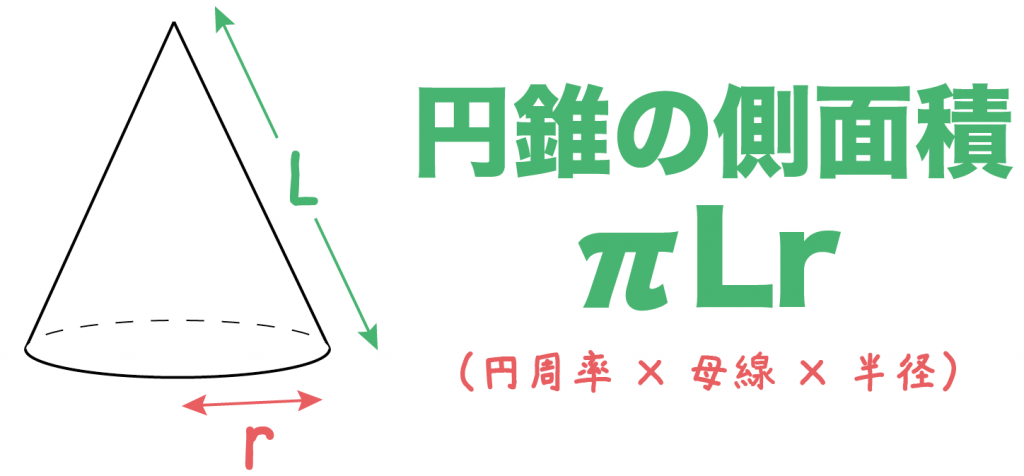



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



U9j580gf8iba369ji2w Xyz P 296




円柱の表面積と体積を求める公式 具体例で学ぶ数学




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




円錐の表面積 あんず学習塾のメモ 図表置き場




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




公式を図解 すい体の体積 円すいの表面積の求め方
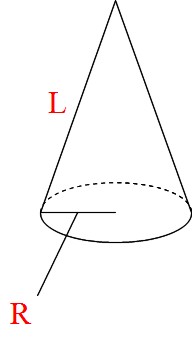



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
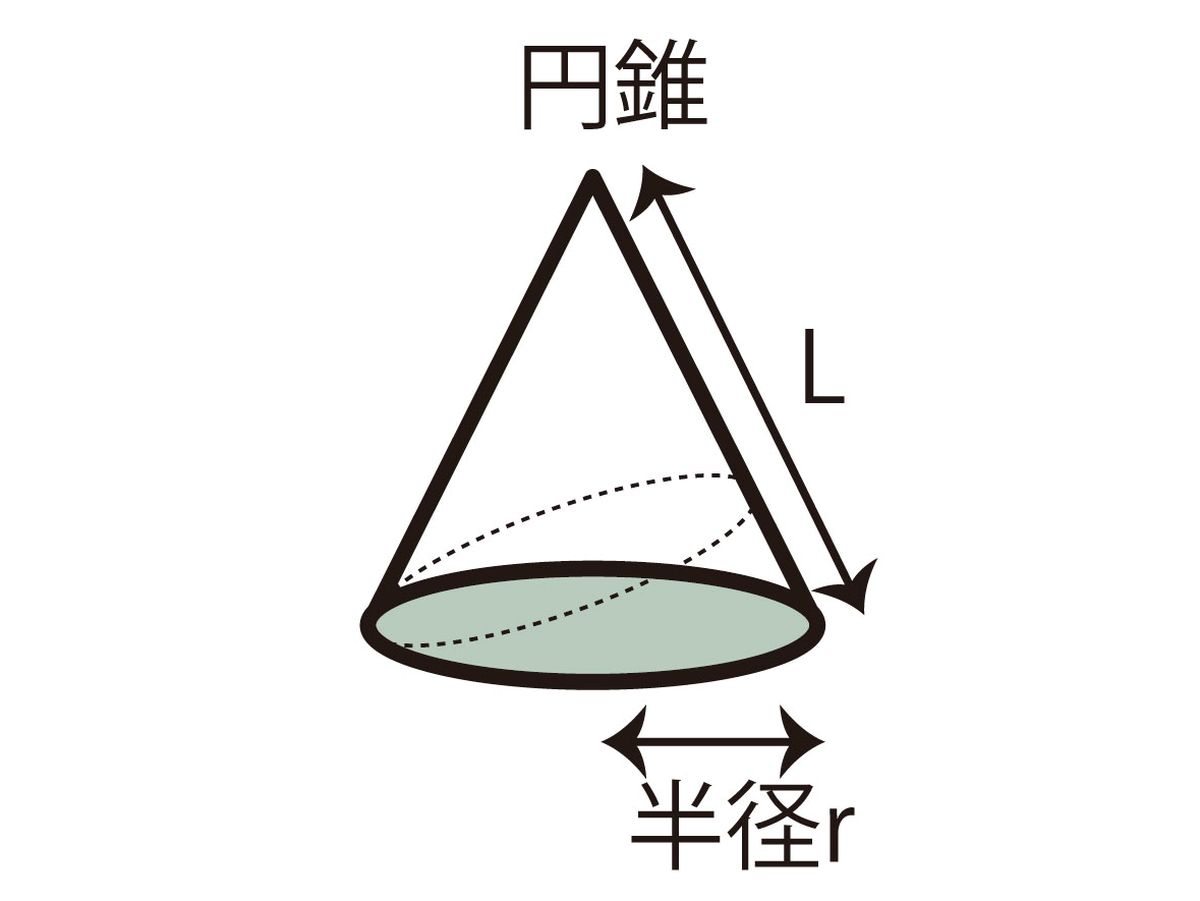



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ




この問題の円錐の底面積の半径の求め方を教えてください Clear



球の表面積の公式の求め方




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
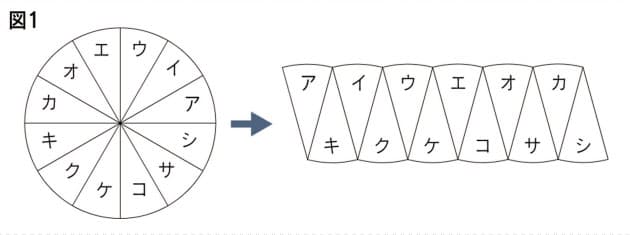



子供に説明できる 円の面積の公式 の証明 Nikkei Style




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



1




球の表面積と体積の公式 数学fun




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




公式を図解 すい体の体積 円すいの表面積の求め方




球の表面積と体積の公式 数学fun




円錐の表面積の求め方 公式と計算例




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




公式を図解 すい体の体積 円すいの表面積の求め方



0 件のコメント:
コメントを投稿